7.1 Entropy
Adapted from Wright
The 1st Law of Thermodynamics states that energy is conserved. It is neither created or destroyed; it is only transferred. This transfer of energy can result in work. For example, a fire heats water to create steam. The steam turns a turbine, performing work, to generate power or move an object.
Now imagine two objects of different temperature that come into contact with each other:
- Object 1: hot - TH
- Object 2: cold - TC
Case 1: Heat (Q) spontaneously flows from the hot object to the cold object until their temperatures reach equilibrium. Energy is conserved.
Case 2: Heat spontaneously flows from the cold object to the hot object. Energy would also be conserved.
In both cases, the 1st law is not violated. However, the second case is never observed in nature.
Energy tends to spread out, or, uniformly distribute itself. In Case 1, the energy distributes itself among both objects. In Case 2, the energy concentrates itself into one one object. The 2nd Law of Thermodynamics, which states that “the total entropy of a system either remains constant or increases in any spontaneous process”, addresses the impossibility of Case #2 (i.e. heat does not spontaneously flow from “cold to hot”) by introducing a new property of a system, entropy, which has many definitions depending on the context.
7.1.1 Uniform Distribution of Energy and Matter
An increase in entropy can be seen with
- The uniform distribution of energy (such as the heat flow shown above)
- The uniform distribution of matter (think of two gases mixing… they will never de-mix)
In both cases, the process of distribution is irreversible, at least in a spontaneous way. Two gases will never un-mix spontaneously. Two objects will never spontaneously un-mix heat (they remain the same temperature).
We say, in both cases, that entropy has increased. The more spread out the energy or matter, the higher the entropy. That means, for the spontaneous, irreversible processes,
\[S_{\mathrm{final}} > S_{\mathrm{initial}}\] Entropy is an extensive property and defined as an amount of heat, q divided by the temperature (and given as J K–1) for a given amount of substance.
\[\Delta S = \dfrac{q}{T}\]
Consider the heat (i.e. the transfer of energy) between the two objects. The hot object with a temperature of TH will experience an average temperature of
\[T_{\mathrm{H,avg}} = \dfrac{T_{\mathrm{H}} + T_{\mathrm{final}}}{2}\]
whereas the cold object with a temperature of TC will experience an average temperature of
\[T_{\mathrm{C,avg}} = \dfrac{T_{\mathrm{C}} + T_{\mathrm{final}}}{2}\] The final temperature for both objects are equal at equilibrium. Therefore,
\[T_{\mathrm{H,avg}} > T_{\mathrm{C,avg}}\]
since the hot object has a higher temperature than the cold object such that
\[T_{\mathrm{H}} > T_{\mathrm{C}}\]
The entropy for the hot object would then be
\[\Delta S_{\mathrm{H}} = \dfrac{-q}{T_{\mathrm{H,avg}}}\]
and the entropy for the cold object would be
\[\Delta S_{\mathrm{C}} = \dfrac{q}{T_{\mathrm{C,avg}}}\]
giving
\[ \Delta S_{\mathrm{H}} < \Delta S_{\mathrm{C}} \]
Since both objects are the system, the entropy for the system would be given as
\[\begin{align*} S_{\mathrm{final}} &= S_{\mathrm{initial}} + \dfrac{-q}{T_{\mathrm{H}}} + \dfrac{q}{T_{\mathrm{C}}} \\[2ex] &= S_{\mathrm{initial}} - \Delta S_{\mathrm{H}} + \Delta S_{\mathrm{C}} \end{align*}\]
Therefore,
\[S_{\mathrm{final}} > S_{\mathrm{initial}}\]
since
\[\Delta S_{\mathrm{H}} < \Delta S_{\mathrm{C}}\]
and the entropy increases for this spontaneous process.
If the direction of heat transfer was from “cold to hot”, the entropy changes would be
\[S_{\mathrm{final}} < S_{\mathrm{initial}}\]
which never occurs spontaneously, thereby violating the 2nd law of thermodynamics.
7.1.2 Predicting Entropy Changes
Below is a table of reactions along with their entropy changes (ΔS°) and energy at room temperature (TΔS° at 298 K). This data and corresponding analyses is taken from Inorganic energetics: An Introduction, 2nd ed.14
The reactions are grouped by:
- Gas phase reactions which result in more particles
- Reactions producing gaseous products from solids or liquids
- Heterogeneous reactions resulting in an increase of gaseous particles
- Gas phase reactions where the number of gas particles do not change
| Reaction | ΔS°298 (J mol–1 K–1) |
TΔS°298 (kJ mol–1) |
|
|---|---|---|---|
(1) |
S8(g) → 8S(g) |
916 |
273 |
Ni(CO)4(g) → Ni(g) + 4CO(g) |
572 |
171 | |
P4(g) → 4P(g) |
372 |
111 | |
N2O4(g) → N2(g) + 2O2(g) |
297 |
89 | |
NH3(g) → ½N2(g) + 1 ½ H2(g) |
99 |
30 | |
NO2(g) → ½N2(g) + O2(g) |
60 |
18 | |
(2) |
NH4Cl(s) → NH3(g) + HCl(g) |
285 |
85 |
NaCl(s) → Na(g) + Cl(g) |
243 |
74 | |
C(s, graphite) + 2S(s, rhombic) → CS2(g) |
168 |
50 | |
H2O(l) → H2(g) + ½O2(g) |
163 |
49 | |
Li(s) + ½I2(s) → LiI(g) |
146 |
44 | |
¼P4(s) + 1½Br2(l) → PBr3(g) |
75 |
22 | |
(3) |
SiCl4(l) + 2H2O(l) → SiO2(s) + 4HCl(g) |
410 |
122 |
AsF3(l) → As(s, gray) + 1½F2(g) |
159 |
47 | |
PbCO3(s) → PbO(s) + CO2(g) |
151 |
45 | |
ZnS(s) + 2H2O(l) → Zn(OH)2(s) + H2S(g) |
91 |
27 | |
NaCl(s) → Na(s) + ½Cl2(g) |
90 |
27 | |
PH3(g) → P(s, white) + 1½H2(g) |
30 |
9 | |
(4) |
½N2(g) + ½O2(g) → NO(g) |
12 |
4 |
½H2(g) + ½I2(g) → HI(g) |
10 |
3 | |
½H2(g) + ½Br2(g) → HBr(g) |
11 |
3 | |
½H2(g) + ½Cl2(g) → HCl(g) |
10 |
3 | |
½H2(g) + ½F2(g) → HF(g) |
7 |
2 | |
½Br2(g) + ½Cl2(g) → BrCl(g) |
6 |
2 | |
½I2(g) + ½Cl2(g) → ICl(g) |
5 |
1 | |
½I2(g) + ½Br2(g) → IBr(g) |
6 |
2 |
In every case where the number of gaseous particles increased, the entropy change is always positive, regardless of the states of any other substance involved in the reaction. In the cases where the number of gaseous particles remained the same (4), the entropy change was very small and close to zero.
Dasent explains why an increase in gas particles leads to an increase in entropy. I will quote the this below.
“One is naturally led to enquire why this should be so. Clearly the standard entropy S°298 of a gas must be high. The reasons for this originate in the discussion of the quantised energy levels of ideal gas molecules given in Sections 1.2.2-4, and can be developed along the following lines.
The entropy of an ideal gas at a given temperature is determined by the number and spacing of the various electronic, vibrational, rotational, and translational energy levels available to the gas. In general, the more distinct ways there are of distributing the molecules throughout the range of available energy levels, the higher will be the entropy. (The entropy may also be affected by configurational or spatial effects and these are discussed at a later stage.) For example, if for some particular component of the energy the quanta are so large that only the ground state is occupied under the given conditions, then there is only one way of assigning the molecules: they all belong to the ground state, and there will be no contribution to the entropy in respect of that particular sort of energy. If, on the other hand, one imagines a hypothetical situation in which (a) for some component E of the energy, a number of equally and closely spaced accessible levels exist, and (b) a sample of four molecules is assigned to these levels, then the following five distributions all give rise to the same total for E.
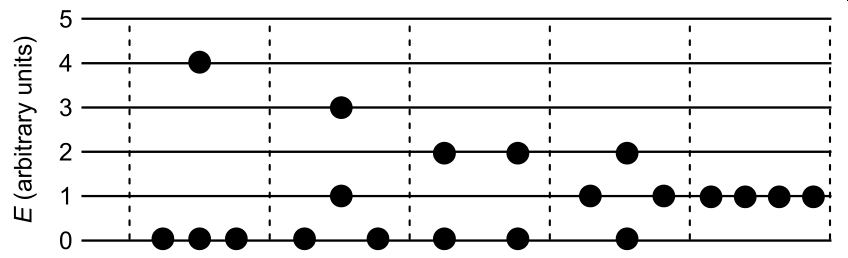
In this simplified situation there are five distinct ways of distributing the molecules among the available energy levels when the energy is spread over a range of quantised levels in this way, a positive contribution to the entropy results.
Thus the very existence of a wide range of accessible energy levels will tend to generate entropy; this is particularly so in the case of the closely spaced rotational levels and a fortiori the translational levels of the ideal gas under consideration.”
So, we see that a system of 4 indistinguishable particles containing 5 units of energy can be arranged in 5 different ways (5 microstates). If there was zero units of available energy, there would only be 1 available configuration of the system (1 microstate; all the particles would be at E = 0). The system with 5 microstates has more entropy than the system with 1 microstate. More microstates (W) means more entropy (S).
\[S = k_{\mathrm{B}}\ln W\]