1.7 Vapor Pressure
Substances naturally exhibit a vapor pressure. This is due to evaporation (i.e. a type of vaporization that takes place at the surface of a liquid), boiling, or sublimation. Substances with non-trivial vapor pressures are volatile whereas those with trivial vapor pressures are nonvolatile and can be approximated to have a vapor pressure of zero.
As a substance vaporizes into a gas, the resulting gas exerts a pressure. A similar occurrence is observed when a substance undergoes boiling. Boiling differs from evaporation such that any particle in the bulk substance can turn into a gas as opposed to those only located at the surface of the substance. Furthermore, boiling occurs when the vapor pressure of the substance equals the external pressure.
Vapor pressure is dependent upon the temperature of the substance. For example, as water is heated, the water molecules gain more kinetic energy. The particles on the surface of the water are better able to escape into the gas phase (i.e. can more easily break the attractive intermolecular forces with neighboring water molecules) at higher temperatures. The relationship between vapor pressure and temperature of a substance based on the heat of vaporization is given by the Clausius-Clapeyron relation (exponential form below)
\[P = Ae^{-\Delta H_{\mathrm{vap}}/RT}\]
where P is the vapor pressure, A is a pre-exponential factor, ΔHvap is the heat of vaporization, R is the gas constant, and T is the temperature. Note that A is substance dependent. As T increases, P increases. The following figure shows vapor pressure curves for some substances.3
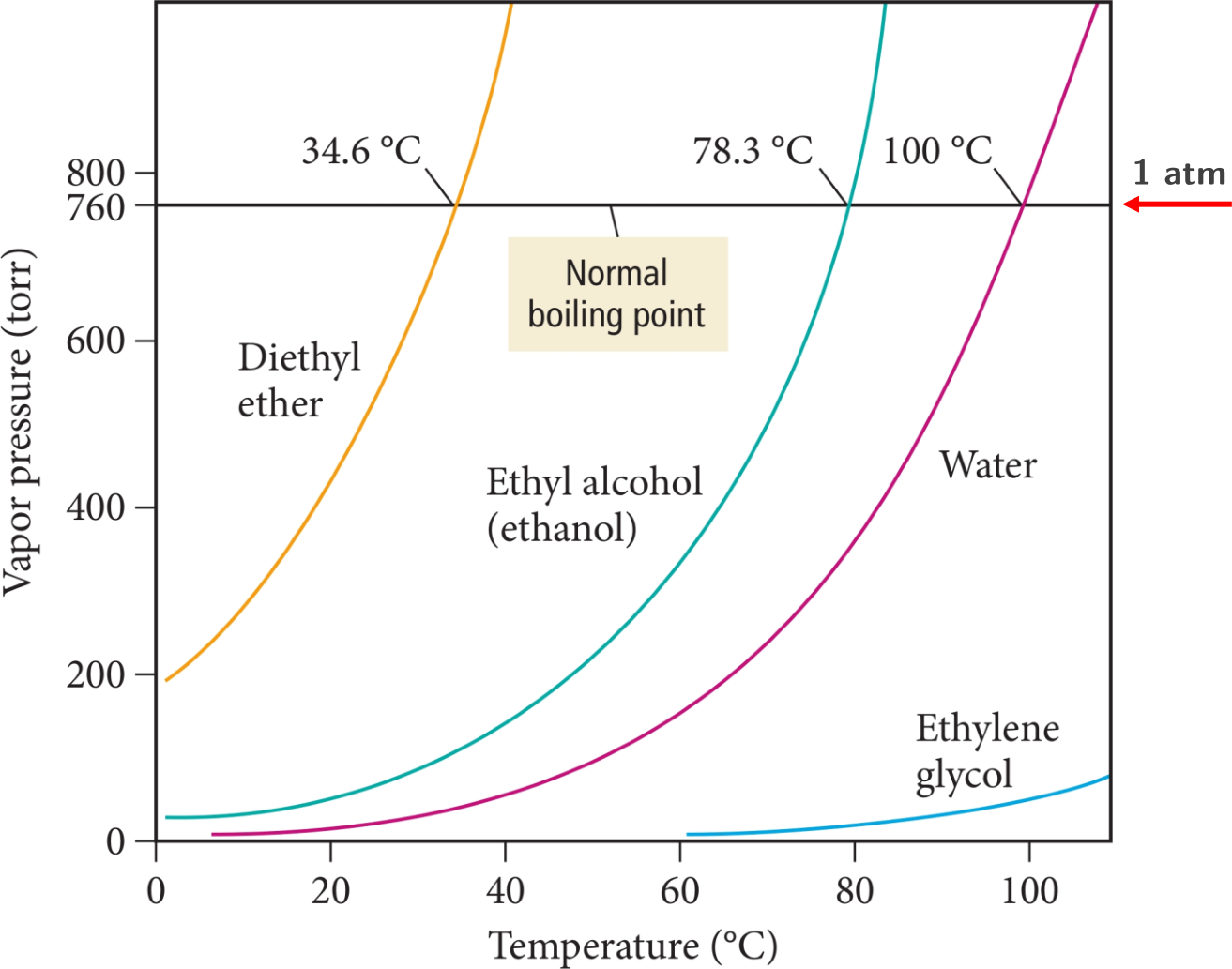
Figure 1.27: Vapor pressure curves for some substances.
Diethyl ether
Ethanol
Water
Ethylene glycol
Notice how vapor pressure increases with increasing temperature. Additionally, one can explain the curves based on intermolecular forces. Water forms up to two hydrogen bonds (i.e. each water molecule can donate two hydrogen bonds) with neighboring water molecules. Ethyl alcohol (i.e. ethanol) can form up to one hydrogen bond and diethyl ether forms weak dipole-dipole interactions. Water requires more energy (higher temperature) to produce an equivalent vapor pressure to diethyl ether or methanol whose IMFs are overall weaker. Diethyl ether and ethanol vaporize more easily relative to water.
Practice
Explain why ethylene glycol exerts much lower vapor pressures than water does across a range of temperatures.
Solution
While ethylene glycol can form up to two hydrogen bonds just like water can, ethylene glycol exhibits more dispersion as it is a larger molecule. This leads to stronger IMFs and therefore lower vapor pressures than water.
The plot below gives the vapor pressure vs. temperature plot for water.
Figure 1.28: Vapor pressure vs. temperature data for water as given by the exponential form of the Clausius-Clapeyron equation.
The data in Figure 1.28 can be transformed to have a linear relationship as given by the linear form of the Clausius-Clapeyron relation:
\[\ln P = -\dfrac{\Delta H_{\mathrm{vap}}}{R}\left ( \dfrac{1}{T} \right ) + \ln A\]
which has the form of a line (i.e. y = mx + b). Note that the slope is
\[\mathrm{slope,}~m = -\dfrac{\Delta H_{\mathrm{vap}}}{R}\]
We can transform the data in Figure 1.28 by taking the natural log of the vapor pressure, ln(P), and the inverse of the temperature, (1/T), to give the following plot (some data points omitted for clarity).
Figure 1.29: Linearized Vapor pressure vs. temperature data for water as given by the linear form of the Clausius-Clapeyron equation
Notice how the data is visually linear. A linear regression of the data points gives the following equation
\[y = -4888.3x + 13.016\]
with a very good coefficient of determination (R2) of 0.9994!
One can estimate the heat of vaporization of water by using the slope of the line such that
\[\begin{align*} \mathrm{slope,}~m &= -\dfrac{\Delta H_{\mathrm{vap}}}{R} = -4888.3 \longrightarrow \\ \Delta H_{\mathrm{vap}} &= -4888.3 \times -R \\ &= -4888.3 \times -(8.314~\mathrm{J~mol^{-1}~K^{-1}}) \left ( \dfrac{\mathrm{kJ}}{10^3~\mathrm{J}} \right ) \\ &= 40.64~\mathrm{kJ~mol^{-1}} \end{align*}\]
This matches the experimental value for water at 100 °C (40.65 kJ mol–1) very well!
Since vapor pressure and temperature data can be linear, we recognize that knowing two points on the line can give the heat of vaporization of water (as well as the slope) and any other point along the line can be determined. This is given by the Clausius-Clapeyron two-point-form equation.
\[\ln \left ( \dfrac{P_2}{P_1} \right ) = \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right )\]
For example, let us take two vapor pressure measurements of water at 25 °C and 50 °C.
| T (°C) | T (K) | P (atm) | |
|---|---|---|---|
1 |
25 |
298.15 |
0.03128 |
2 |
50 |
323.15 |
0.1219 |
We can now solve for the heat of vaporization.
\[\begin{align*} \ln \left ( \dfrac{P_2}{P_1} \right ) &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right ) \longrightarrow \\[2ex] \Delta H_{\mathrm{vap}} &= R\left (\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{1}{T_1} - \dfrac{1}{T_2}} \right )\\ \Delta H_{\mathrm{vap}} &= (8.314~\mathrm{J~mol^{-1}~K^{-1}}) \left (\dfrac{\ln \left ( \dfrac{0.1219~\mathrm{atm}}{0.03128~\mathrm{atm}} \right )} {\dfrac{1}{298.15~\mathrm{K}} - \dfrac{1}{323.15~\mathrm{K}}}\right ) \left ( \dfrac{\mathrm{kJ}}{10^3~\mathrm{J}} \right ) \\ &= 43.58~\mathrm{kJ~mol^{-1}} \end{align*}\]
While this value does not exactly match the experimental value, it is rather close and demonstrates the utility behind this approximation!
You should be able to solve for any variable in these equations. The algebra for isolating each term is given below.
ΔHvap
\[\begin{align} \ln \left ( \dfrac{P_2}{P_1} \right ) &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right )\\[4ex] \dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{1}{T_1} - \dfrac{1}{T_2}} &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \\[2ex] R\left (\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{1}{T_1} - \dfrac{1}{T_2}} \right ) &= \Delta H_{\mathrm{vap}} \\[2ex] \Delta H_{\mathrm{vap}} &= R\left (\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{1}{T_1} - \dfrac{1}{T_2}} \right ) \\[2ex] \mathrm{or}\\[2ex] \Delta H_{\mathrm{vap}} &= R\left (\dfrac{\ln P_2 - \ln P_1}{\dfrac{1}{T_1} - \dfrac{1}{T_2}} \right ) \end{align}\]
P1
\[\begin{align} \ln \left ( \dfrac{P_2}{P_1} \right ) &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right )\\[4ex] \ln P_2 - \ln P_1 &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right )\\[2ex] - \ln P_1 &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right ) - \ln P_2\\[2ex] \ln P_1 &= -\dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right ) + \ln P_2\\[2ex] e^{(\ln P_1)} &= e^{\left(-\frac{\Delta H_{\mathrm{vap}}}{R} \left ( \frac{1}{T_1} - \frac{1}{T_2} \right ) + \ln P_2\right)}\\[2ex] P_1 &= e^{\left(-\frac{\Delta H_{\mathrm{vap}}}{R} \left ( \frac{1}{T_1} - \frac{1}{T_2} \right ) + \ln P_2\right)} \end{align}\]
P2
\[\begin{align*} \ln \left ( \dfrac{P_2}{P_1} \right ) &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right )\\[4ex] \ln P_2 - \ln P_1 &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right )\\[2ex] \ln P_2 &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right ) + \ln P_1\\[2ex] e^{(\ln P_2)} &= e^{\left(\frac{\Delta H_{\mathrm{vap}}}{R} \left ( \frac{1}{T_1} - \frac{1}{T_2} \right ) + \ln P_1\right)}\\[2ex] P_2 &= e^{\left(\frac{\Delta H_{\mathrm{vap}}}{R} \left ( \frac{1}{T_1} - \frac{1}{T_2} \right ) + \ln P_1\right)} \end{align*}\]
T1
\[\begin{align*} \ln \left ( \dfrac{P_2}{P_1} \right ) &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right )\\[4ex] \dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{\Delta H_{\mathrm{vap}}}{R}} &= \dfrac{1}{T_1} - \dfrac{1}{T_2} \\[2ex] \dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{\Delta H_{\mathrm{vap}}}{R}} + \dfrac{1}{T_2} &= \dfrac{1}{T_1} \\[2ex] \dfrac{1}{\left (\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{\Delta H_{\mathrm{vap}}}{R}} + \dfrac{1}{T_2}\right )} &= T_1 \\[2ex] T_1 &= \dfrac{1}{\left (\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{\Delta H_{\mathrm{vap}}}{R}} + \dfrac{1}{T_2}\right ) } \end{align*}\]
T2
\[\begin{align*} \ln \left ( \dfrac{P_2}{P_1} \right ) &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right )\\[4ex] \dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{\Delta H_{\mathrm{vap}}}{R}} &= \dfrac{1}{T_1} - \dfrac{1}{T_2} \\[2ex] \dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{\Delta H_{\mathrm{vap}}}{R}} - \dfrac{1}{T_1} &= -\dfrac{1}{T_2} \\[2ex] -\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{\Delta H_{\mathrm{vap}}}{R}} + \dfrac{1}{T_1} &= \dfrac{1}{T_2} \\[2ex] \dfrac{1}{\left ( -\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{\Delta H_{\mathrm{vap}}}{R}} + \dfrac{1}{T_1} \right )} &= T_2 \\[2ex] T_2 &= \dfrac{1}{\left (-\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{\Delta H_{\mathrm{vap}}}{R}} + \dfrac{1}{T_1}\right )} \end{align*}\]
Practice
What is the heat of vaporization of water (in kJ mol–1) if the vapor pressure of water at 10 °C is 0.01212 atm and at 80 °C is 0.46794 atm?
Solution
Convert T into Kelvin.
\[\begin{align*} T_1 = 273.15 + 10~^{\circ}\mathrm{C} = 283.15~\mathrm{K}~(\text{at 0.01212 atm})\\[2.0ex] T_1 = 273.15 + 80~^{\circ}\mathrm{C} = 353.15~\mathrm{K}~(\text{at 0.46794 atm}) \end{align*}\]
Solve for the heat of vaporization
\[\begin{align*} \ln \left ( \dfrac{P_2}{P_1} \right ) &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right ) \longrightarrow \\[2ex] \Delta H_{\mathrm{vap}} &= R\left (\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{1}{T_1} - \dfrac{1}{T_2}} \right )\\ \Delta H_{\mathrm{vap}} &= (8.314~\mathrm{J~mol^{-1}~K^{-1}}) \left (\dfrac{\ln \left ( \dfrac{0.46794~\mathrm{atm}}{0.01212~\mathrm{atm}} \right )} {\dfrac{1}{283.15~\mathrm{K}} - \dfrac{1}{353.15~\mathrm{K}}}\right ) \left ( \dfrac{\mathrm{kJ}}{10^3~\mathrm{J}} \right ) \\ &= 43.39~\mathrm{kJ~mol^{-1}} \end{align*}\]
Math String: 8.314 * ln(0.46794/0.01212) / ((1/283.15) - (1/353.15)) / 1000
Practice
A substance is found to have a vapor pressure of 244.34 mmHg at 25 °C. If the heat of vaporization of the substance was 18.35 kJ mol–1, what is the vapor pressure of the substance (in mmHg) at 45 °C?
Solution
Convert T into Kelvin.
\[\begin{align*} T_1 &= 273.15 + 25~^{\circ}\mathrm{C} = 298.15~\mathrm{K}~\text{(at 244.34 mmHg)} \\[2ex] T_2 &= 273.15 + 45~^{\circ}\mathrm{C} = 318.15~\mathrm{K} \end{align*}\]
Convert ΔHvap into J mol–1.
\[\begin{align*} \Delta H_{\mathrm{vap}} &= 18.35~\mathrm{kJ~mol^{-1}} \left ( \dfrac{10^3~\mathrm{J}}{\mathrm{kJ}} \right ) \\ &= 18,350~\mathrm{J~mol^{-1}} \end{align*}\]
Solve for P2.
\[\begin{align*} \ln \left ( \dfrac{P_2}{P_1} \right ) &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right ) \longrightarrow \\[4ex] P_2 &= e^{\left(\frac{\Delta H_{\mathrm{vap}}}{R} \left ( \frac{1}{T_1} - \frac{1}{T_2} \right ) + \ln P_1\right)} \\ &= e^{\left(\frac{18,350~\mathrm{J~mol^{-1}}}{8.314~\mathrm{J~mol^{-1}~K^{-1}}} \left ( \frac{1}{298.15~\mathrm{K}} - \frac{1}{318.15~\mathrm{K}} \right ) + \ln ( 244.34~\mathrm{mmHg} ) \right ) } \\ &= 389.13~\mathrm{mmHg} \end{align*}\]
Math String: e^(18350/8.314 * ((1/298.15) - (1/318.15)) + ln(244.34))
Practice
A liquid (m.w. = 148.511 g mol–1) is vaporized. The liquid is found to exert a vapor pressure of 0.344 atm at -82 °C. At -12 °C, the vapor pressure was 2.340 atm. How much heat (in kJ) is required to vaporize 5.0 kg of the liquid?
Solution
We use Clausius-Clapeyron two-point form to determine the heat of vaporization for the liquid.
Convert T into Kelvin.
\[\begin{align*} T_1 &= 273.15 + -82~^{\circ}\mathrm{C} = 191.15~\mathrm{K}~(\text{at 0.344 atm})\\ T_2 &= 273.15 + -12~^{\circ}\mathrm{C} = 261.15~\mathrm{K}~(\text{at 2.340 atm}) \end{align*}\]
Solve for ΔHvap.
\[\begin{align*} \ln \left ( \dfrac{P_2}{P_1} \right ) &= \dfrac{\Delta H_{\mathrm{vap}}}{R} \left ( \dfrac{1}{T_1} - \dfrac{1}{T_2} \right ) \longrightarrow \\[2ex] \Delta H_{\mathrm{vap}} &= R\left (\dfrac{\ln \left ( \dfrac{P_2}{P_1} \right )}{\dfrac{1}{T_1} - \dfrac{1}{T_2}} \right )\\ \Delta H_{\mathrm{vap}} &= (8.314~\mathrm{J~mol^{-1}~K^{-1}}) \left (\dfrac{\ln \left ( \dfrac{2.340~\mathrm{atm}}{0.344~\mathrm{atm}} \right )} {\dfrac{1}{191.15~\mathrm{K}} - \dfrac{1}{261.15~\mathrm{K}}}\right ) \left ( \dfrac{\mathrm{kJ}}{10^3~\mathrm{J}} \right ) \\ &= 11.37~\mathrm{kJ~mol^{-1}} \end{align*}\]
Math String: 8.314 * ln(2.340/0.344) / ((1/191.15) - (1/261.15)) / 1000
Find the amount of heat (q in kJ) required to vaporize 5.0 kg of the liquid.
\[\begin{align*} q &= m \times \text{molar mass} \times \Delta H_{\mathrm{vap}} \\[2ex] &= 5.0~\mathrm{kg} \left ( \dfrac{10^3~\mathrm{g}}{\mathrm{kg}} \right ) \left ( \dfrac{\mathrm{mol}}{148.511~\mathrm{g}} \right ) \left ( \dfrac{11.37~\mathrm{kJ}}{\mathrm{mol}} \right ) \\[2ex] &= 382.8~\mathrm{kJ} \end{align*}\]
Recall the p–T diagram for water.
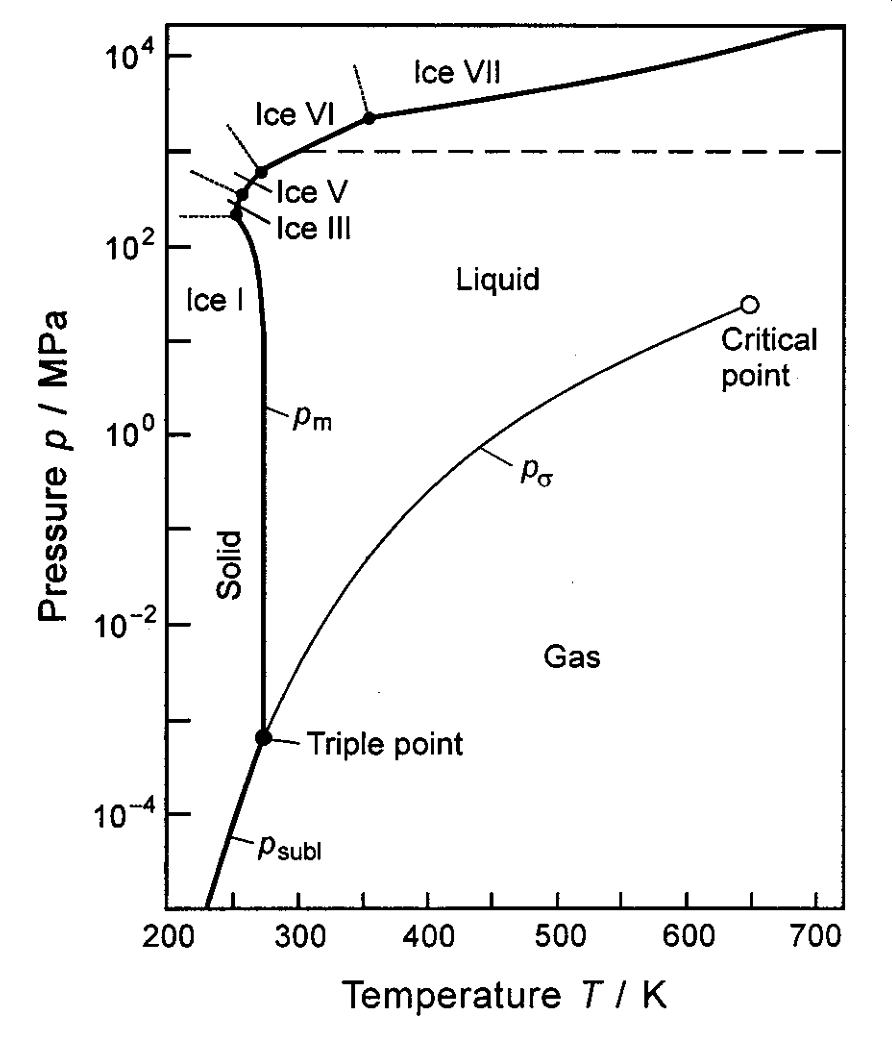
Figure 1.30: The p–T diagram for water
The liquid-gas boundary is closely matched by the Clausius-Clapeyron relation. Taking the data from 1.28 and transforming the y-axis to be on a log10 scale gives
Figure 1.31: Vapor pressure vs. temperature for water