3.5 Half-life
The half-life (t1/2) for any reaction is simply the amount of time required for exactly one half of the reactant to be consumed. Given that each order of reaction responds differently to reactant concentration, the half-life for these reactions vary. We can easily derive the half-life equations from their integrated rate law counterparts.
To perform the derivation, simply start with an appropriate integrated rate law. Make the following modifications to the equation
\[t ~\longrightarrow~ t_{1/2}\] and
\[[\mathrm{A}]_t ~\longrightarrow~ \dfrac{1}{2}[\mathrm{A}]_0\] since, by definition, the half-life of a reaction is when exactly one half of the reactant concentration is consumed. Once that is done, solve for t1/2.
Zeroth-order Half-life
\[t_{1/2} = \dfrac{[\mathrm{A}]_0}{2k}\]
Derivation
\[\begin{align*} [\mathrm{A}]_t &= -kt + [\mathrm{A}]_0 \\ \frac{1}{2}[\mathrm{A}]_0 &= -kt_{1/2} + [\mathrm{A}]_0 \\ kt_{1/2} &= [\mathrm{A}]_0 - \frac{1}{2}[\mathrm{A}]_0 \\ t_{1/2} &= \dfrac{[\mathrm{A}]_0}{2k} \end{align*}\]
First-order Half-life
\[\begin{align*} t_{1/2} &= \dfrac{\ln 2}{k}\\[1.5ex] &\approx \dfrac{0.693}{k} \end{align*}\]
Derivation
\[\begin{align*} \ln\mathrm{[A]}_t &= -kt + \ln\mathrm{[A]_0} \\[1.5ex] \ln \left (\frac{1}{2}[\mathrm{A}]_0 \right ) &= -kt_{1/2} + \ln\mathrm{[A]_0}\\[1.5ex] \ln \left (\frac{1}{2}[\mathrm{A}]_0 \right ) - \ln\mathrm{[A]_0} &= -kt_{1/2} \\[1.5ex] \ln\left ( \dfrac{\frac{1}{2}[\mathrm{A}]_0}{[\mathrm{A}]_0} \right ) &= -kt_{1/2} \\[1.5ex] \ln\dfrac{1}{2} &= -kt_{1/2} \\[1.5ex] t_{1/2} &= -\dfrac{\ln\frac{1}{2}}{k} \\[1.5ex] &= \dfrac{\ln 2}{k}\\[1.5ex] & = \dfrac{0.693}{k} \end{align*}\]
Second-order Half-life
\[t_{1/2} = \dfrac{1}{k[\mathrm{A}]_0}\]
Derivation
\[\begin{align*} \dfrac{1}{[\mathrm{A}]_t} &= kt + \dfrac{1}{[\mathrm{A}]_0} \\ \dfrac{1}{\frac{1}{2}[\mathrm{A}]_0} &= kt_{1/2} + \dfrac{1}{[\mathrm{A}]_0} \\ \dfrac{2}{[\mathrm{A}]_0} - \dfrac{1}{[\mathrm{A}]_0}&= kt_{1/2} \\ \dfrac{1}{[\mathrm{A}]_0}&= kt_{1/2} \\ \dfrac{1}{k[\mathrm{A}]_0}&= t_{1/2} \\ t_{1/2} &= \dfrac{1}{k[\mathrm{A}]_0} \end{align*}\]
The plot below illustrates the half-life for a first-order reaction with k = t–1.
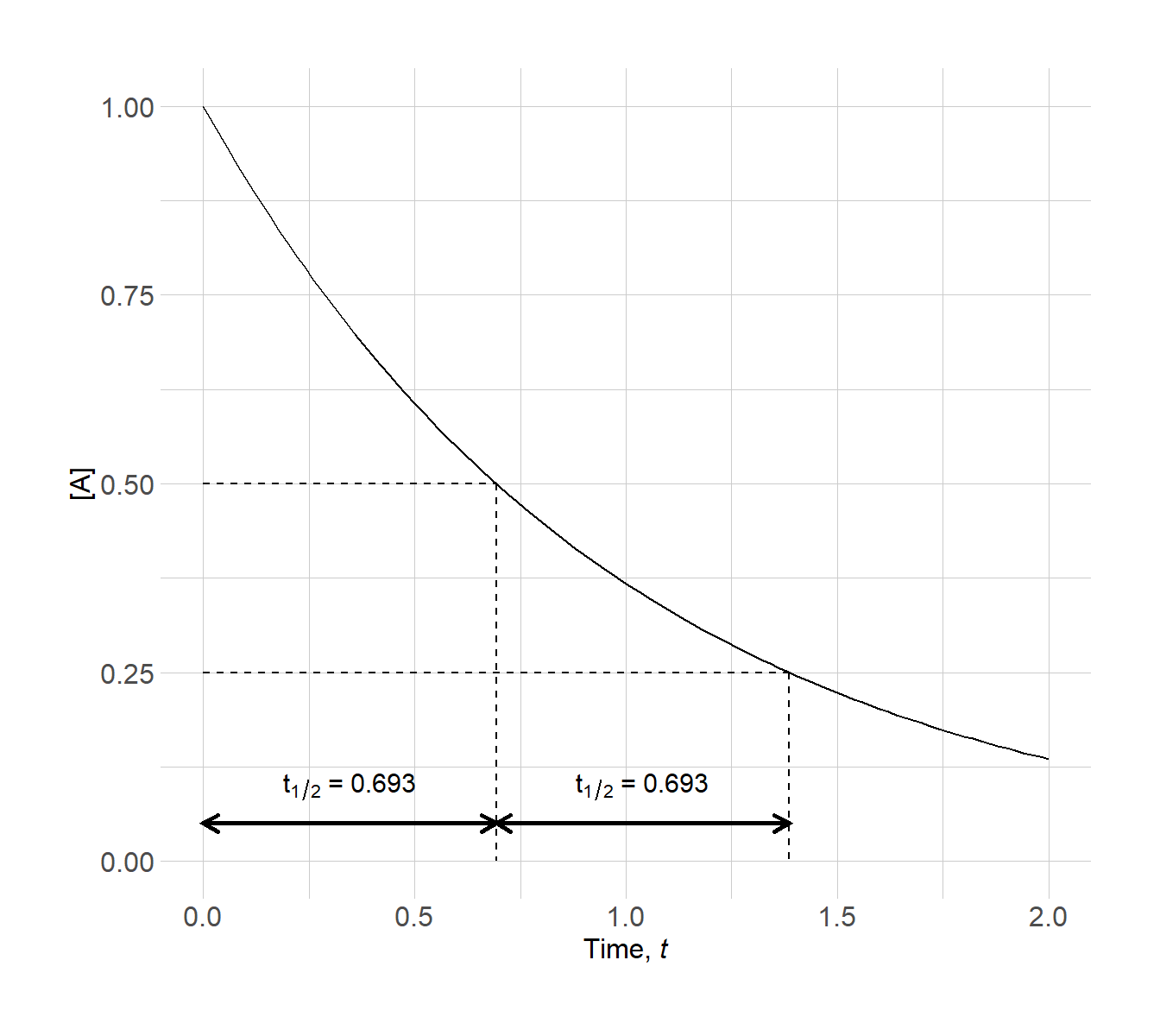
Figure 3.19: Half-life plot for a first-order reaction
Notice that each time required for exactly half of the reactant concentration to be consumed. The half-life does not change with reactant concentration.
Practice
Let us continue using our reaction from above. The reaction has a rate constant of 0.3387 M–1 s–1 (at 326.86 °C or 600 K) and begins with 5.0 M NO2.
\[2\mathrm{NO_2}(g) \longrightarrow \mathrm{2NO}(g) + \mathrm{O_2}(g)\]
What is the half-life (in s) of the reaction?
Solution
We resort to the second-order half-life equation to solve this. Solve for t1/2 (in s).
\[\begin{align*} t_{1/2} &= \dfrac{1}{k[\mathrm{A}]_0} \\[1.5ex] &= \dfrac{1}{0.3387~M^{-1}~\mathrm{s}^{-1} \left ( 5.0~M \right )} \\[1.5ex] &= 0.5905~\mathrm{s} \end{align*}\]
Therefore, half the NO2 concentration gets consumed about every sixth of a second.
Extend
Does the half-life change with a different initial concentration?
For a second-order reaction it does! Let’s determine the half-life of the reaction if the initial concentration was 1.0 M.
Solve
\[\begin{align*} t_{1/2} &= \dfrac{1}{k[\mathrm{A}]_0} \\[1.5ex] &= \dfrac{1}{0.3387~M^{-1}~\mathrm{s}^{-1} \left ( 1.0~M \right )} \\[1.5ex] &= 2.952~\mathrm{s} \end{align*}\]
Because a second-order reaction has a rate that slows exponentially with reactant consumption, the half-life increases with decreasing rate!
Plot
Let’s visualize the change in half-life as reactant gets consumed.
Figure 3.20: Half-life plot for this second-order reaction.
As expected, the half-life increases with reaction progress (e.g. as NO2 gets consumed).
Follow Through
So we see that the half-life changes as a second-order reaction progresses. Will the half-life change as a zeroth-order reaction progresses? What about a first-order reaction?